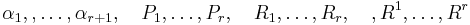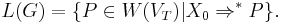Matrix grammar
A matrix grammar is a formal grammar in which instead of single productions, productions are grouped together into finite sequences. A production cannot be applied separately, it must be applied in sequence. In the application of such a sequence of productions, the rewriting is done in accordance to the each production in sequence, the first one, second one etc. till the last production has been used for rewriting. The sequences are referred to as matrices.
Matrix grammar is an extension of context-free grammar, and one instance of a Controlled grammar.
Formal definition
A matrix grammar is an ordered quadruple
where
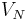 is a finite set of non-terminals
is a finite set of non-terminals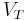 is a finite set of terminals
is a finite set of terminals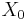 is a special element of
is a special element of 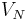 , viz. the starting symbol
, viz. the starting symbol is a finite set of non-empty sequences whose elements are ordered pairs
is a finite set of non-empty sequences whose elements are ordered pairs
The pairs are called productions, written as 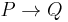 . The sequences are called matrices and can be written as
. The sequences are called matrices and can be written as
Let  be the set of all productions appearing in the matrices
be the set of all productions appearing in the matrices  of a matrix grammar
of a matrix grammar  . Then the matrix grammar
. Then the matrix grammar  is of type-
is of type-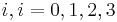 , length-increasing, linear,
, length-increasing, linear,  -free, context-free or context-sensitive if and only if the grammar
-free, context-free or context-sensitive if and only if the grammar 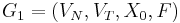 has the following property.
has the following property.
For a matrix grammar  , a binary relation
, a binary relation 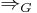 is defined; also represented as
is defined; also represented as 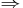 . For any
. For any 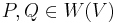 ,
, 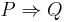 holds if and only if there exists an integer
holds if and only if there exists an integer 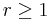 such that the words
such that the words
over V exist and
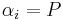 and
and 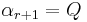
 is one of the matrices of
is one of the matrices of 
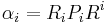 and
and 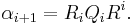
If the above conditions are satisfied, it is also said that 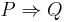 holds with
holds with 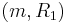 as the specifications.
as the specifications.
Let 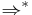 be the reflexive transitive closure of the relation
be the reflexive transitive closure of the relation 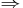 . Then, the language generated by the matrix grammar
. Then, the language generated by the matrix grammar  is given by
is given by
Example
Consider the matrix grammar
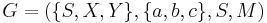
where  is a collection containing the following matrices:
is a collection containing the following matrices:
![[S \rightarrow XY], \quad [X \rightarrow aXb, Y \rightarrow cY], \quad [X \rightarrow ab, Y \rightarrow c]](/2012-wikipedia_en_all_nopic_01_2012/I/39ebeeb9c961971a919cc346377a6710.png)
These matrices, which contain only context-free rules generate the context-sensitive language
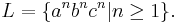
This example can be found on pages 8 and 9 of [1].
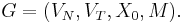
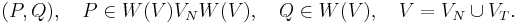
![m = [P_1 \to Q_1, \ldots, P_r \to Q_r].](/2012-wikipedia_en_all_nopic_01_2012/I/32440b2e8794137143d3ebf49248340d.png)